


Next: Analyses d'association
Up: Méthodes utilisées
Previous: Méthodes utilisées
Contents
Analyse de liaison paramétrique ou méthode des lod-scores
Le but des analyses de liaison (paramétriques ou non paramétriques) est de localiser les régions contenant les gènes responsables du trait ou de la maladie sur le génome au moyen d'observations sur des individus reliés. La méthode des lod-scores est basée sur la co-ségrégation, au cours des générations, des allèles de marqueurs polymorphes avec le locus responsable de la maladie (ou du trait), dans une ou un échantillon de familles [Demenais et al., 1996,Feingold et al., 1998,Campion, 2001]. Cette co-ségrégation est due à l'existence d'une liaison génétique entre ces deux loci (gène-marqueur). Deux loci (marqueur-marqueur/ gène-marqueur) sont dits "liés" s'ils sont suffisamment proches l'un de l'autre sur le même chromosome pour être cohérités dans plus de 50% des cas. Cette liaison est dépendante d'un événement biologique de la méiose qui casse la co-ségrégation, la recombinaison intra-chromosomique ("crossing-over"). Deux loci sont rarement disjoints par un événement de recombinaison si la distance physique entre les deux loci est suffisamment faible. L'analyse de liaison repose donc sur la fraction de recombinaison 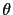 (la probabilité de recombinaison entre deux loci à la méiose) qui est fonction de la distance entre les loci. Cette distance est exprimée en unité de recombinaison ou centiMorgan : 1 cM correspond à une fréquence de recombinaison de 1% entre les deux loci. Si
(la probabilité de recombinaison entre deux loci à la méiose) qui est fonction de la distance entre les loci. Cette distance est exprimée en unité de recombinaison ou centiMorgan : 1 cM correspond à une fréquence de recombinaison de 1% entre les deux loci. Si 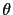 =0, les deux loci sont co-hérités dans 100% des cas (liaison parfaite). La distance génétique entre les deux loci est alors de 0 cM. Si
=0, les deux loci sont co-hérités dans 100% des cas (liaison parfaite). La distance génétique entre les deux loci est alors de 0 cM. Si 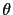 =0.5, les deux loci sont génétiquement indépendants en termes de ségrégation. Les deux loci se situent soit sur deux chromosomes différents soit sont à une distance suffisamment grande sur le même chromosome (>50 cM). L'analyse de liaison repose sur le logarithme du rapport de vraisemblance entre deux hypothèses (l'hypothèse à tester versus l'hypothèse nulle). Le degré de la liaison génétique, exprimée en lod score (Z) par Morton (1955), est obtenue par le logarithme décimal du rapport entre la vraisemblance de liaison (l'hypothèse alternative) entre le marqueur (position connue) et le gène de la maladie (position inconnue) pour une distance génétique donnée, représentée par le taux de recombinaison
=0.5, les deux loci sont génétiquement indépendants en termes de ségrégation. Les deux loci se situent soit sur deux chromosomes différents soit sont à une distance suffisamment grande sur le même chromosome (>50 cM). L'analyse de liaison repose sur le logarithme du rapport de vraisemblance entre deux hypothèses (l'hypothèse à tester versus l'hypothèse nulle). Le degré de la liaison génétique, exprimée en lod score (Z) par Morton (1955), est obtenue par le logarithme décimal du rapport entre la vraisemblance de liaison (l'hypothèse alternative) entre le marqueur (position connue) et le gène de la maladie (position inconnue) pour une distance génétique donnée, représentée par le taux de recombinaison 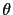 (0
(0
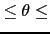 0.5) et l'hypothèse d'indépendance génétique entre ce marqueur et le gène recherché (hypothèse nulle,
0.5) et l'hypothèse d'indépendance génétique entre ce marqueur et le gène recherché (hypothèse nulle, 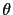 =0.5): Z(
=0.5): Z(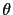 )=
)= 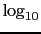 [L(
[L(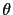 )/L(0.5)] [Morton, 1955]. L'analyse de liaison teste la vraisemblance d'une liaison génétique pour diverses valeurs de recombinaison
)/L(0.5)] [Morton, 1955]. L'analyse de liaison teste la vraisemblance d'une liaison génétique pour diverses valeurs de recombinaison 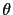 voisines de zéro et pour un marqueur donné. Le lod score varie donc suivant la valeur de
voisines de zéro et pour un marqueur donné. Le lod score varie donc suivant la valeur de 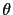 considérée. Plus le lod score est élevé, plus la probabilité de la liaison entre le marqueur et le gène causal est grande et inversement. Classiquement, l'hypothèse d'indépendance est rejetée avec un score Z(
considérée. Plus le lod score est élevé, plus la probabilité de la liaison entre le marqueur et le gène causal est grande et inversement. Classiquement, l'hypothèse d'indépendance est rejetée avec un score Z(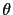 ) supérieur à 3 (correspondant à P=10
) supérieur à 3 (correspondant à P=10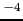 ). Il y a alors liaison génétique (ou "linkage" en anglais) entre le marqueur et la maladie. L'hypothèse de liaison est rejetée si Z(
). Il y a alors liaison génétique (ou "linkage" en anglais) entre le marqueur et la maladie. L'hypothèse de liaison est rejetée si Z(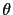 )<-2. Cela signifie qu'il y a une preuve que des événements de recombinaison ont eu lieu entre le marqueur et le locus maladie. Pour un lod score entre ces deux valeurs, on ne peut pas conclure ni à une liaison ni à une exclusion, il faut analyser d'autres familles. Dans le cas de stratégie "genome-wide scan", le seuil monte à 3.3 pour conclure à une liaison avec une valeur de P de 0.05 [Lander and Kruglyak, 1995].
)<-2. Cela signifie qu'il y a une preuve que des événements de recombinaison ont eu lieu entre le marqueur et le locus maladie. Pour un lod score entre ces deux valeurs, on ne peut pas conclure ni à une liaison ni à une exclusion, il faut analyser d'autres familles. Dans le cas de stratégie "genome-wide scan", le seuil monte à 3.3 pour conclure à une liaison avec une valeur de P de 0.05 [Lander and Kruglyak, 1995].
L'objectif final de l'analyse est d'estimer la fraction de recombinaison (ou la position chromosomique (cM)) entre chaque marqueur et le locus de la maladie (analyse bi-point) ou la position du locus de la maladie relative à une carte fixe des marqueurs où l'on suppose que l'endroit de chaque marqueur est connu (analyse multipoint). L'analyse multipoint peut être plus puissante car l'informativité d'un marqueur peut être améliorée en le considérant simultanément avec les marqueurs voisins. Elle permet aussi d'avoir une estimation de la localisation du locus "maladie" et de se protéger contre les résultats abérrants obtenus pour un marqueur. Cependant, elle reste sensible à la présence d'erreurs de génotypage et elle requiert un ordre correct des marqueurs ainsi que de la distance entre les marqueurs. La meilleure estimation (le maximum de vraisemblance) de 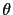 ou de la position est celle qui maximise la fonction du lod score: le lod score maximum. De plus, même si cette analyse est basée sur l'existence d'un locus majeur à l'origine du trait, elle peut également prendre en compte l'hétérogénéité génétique à l'aide du paramètre
ou de la position est celle qui maximise la fonction du lod score: le lod score maximum. De plus, même si cette analyse est basée sur l'existence d'un locus majeur à l'origine du trait, elle peut également prendre en compte l'hétérogénéité génétique à l'aide du paramètre 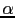 qui répartit les familles en familles liées et non liées au marqueur considéré.Le lod score est alors maximisé en fonction des paramètres
qui répartit les familles en familles liées et non liées au marqueur considéré.Le lod score est alors maximisé en fonction des paramètres 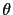 et
et 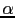 (la proportion de familles liées au locus étudié). Ce lod score, intitulé "HLOD" (heterogeneity LOD) est défini comme étant:
(la proportion de familles liées au locus étudié). Ce lod score, intitulé "HLOD" (heterogeneity LOD) est défini comme étant:
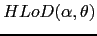 =
=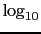 [L(
[L(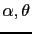 )/L(
)/L(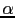 =1,
=1,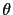 =0.5)].
=0.5)].
Les analyses de liaison paramétrées sont réalisées avec différents programmes comme Linkage [Lathrop et al., 1984], GeneHunter [Kruglyak et al., 1996], Merlin [Abecasis et al., 2002], Simwalk2 [Sobel and Lange, 1996], qui utilisent divers algorithmes (Elston-Stewart, Lander-Green, chaines de Markov Monte Carlo) pour permettre d'étudier de nombreux marqueurs dans des familles de toutes tailles.
Cette méthode est très puissante surtout lors de son application à l'étude de plusieurs grandes généalogies où un même gène majeur, quels que soient les allèles impliqués, est à l'origine de la maladie. En effet, dans les études de liaison génétique, l'existence d'une hétérogénéité allélique n'affecte pas l'analyse car toutes les familles (avec différentes mutations) montreront une liaison avec la même région chromosomique. Selon les familles, différents allèles d'un même marqueur seront alors liés à la maladie. Elle fut d'ailleurs largement utilisée pour cartographier de nombreux gènes impliqués dans des maladies mendéliennes. Dans ce cas, l'étude de grandes familles est vraiment intéressante car il y a une très forte probabilité pour que l'ensemble des cas développés au sein d'une même famille soit dû à une susceptibilité commune. Cependant, cette méthode reste peu adaptée dans le cas des maladies complexes avec hétérogénéité non allélique. Etant une méthode paramétrée, elle nécessite la connaissance du modèle génétique (mode de transmission) de la maladie, c'est-à-dire si la maladie est autosomique ou liée au chromosome X, si elle est dominante ou récessive. Elle dépend de la fréquence et de la pénétrance de l'allèle de prédisposition à la maladie, de la fréquence des phénocopies, du taux de mutation et de la fréquence allélique des marqueurs de la maladie. Ces paramètres sont souvent préalablement estimés par les études de ségrégation. De manière générale, elle dépend aussi de la famille étudiée, sa taille et sa composition en nombre d'individus atteints, et des marqueurs microsatellites selon leur informativité (degré de polymorphisme). Dans le cas des maladies complexes, le mode héréditaire de transmission de la maladie est souvent trop imprécis. La méconnaissance de ces paramètres conduit généralement à une perte de puissance pour détecter une liaison existante (faux négatifs) et/ou à détecter par hasard une liaison inexistante (faux positifs). A moins d'avoir montré lors d'une analyse de ségrégation l'implication d'un gène majeur, il serait peu adapté d'utiliser cette méthode dans l'étude des maladies complexes.
Analyse de liaison non paramétrique ou méthode des paires de
germains
Pour les raisons précédemment décrites, d'autres méthodes, dites non paramétri-
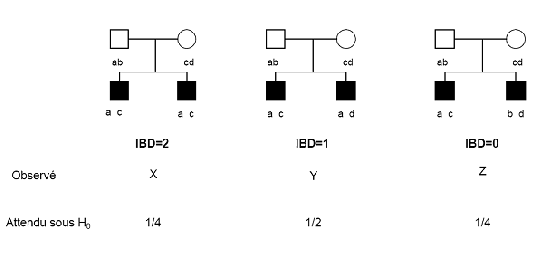
Figure 1.5:
Différents états IBD possibles pour une paire de germains atteints
IBD: identique par descendance, IBD0: aucun allèle IBD, IBD1: un allèle IBD commun,
et IBD2: deux allèles IBD commun entre les germains
 |
ques (ou "model-free") peuvent être utilisées [Demenais et al., 1996,Seboun, 1996,Feingold et al., 1998,Campion, 2001,Feingold, 2005]. Elles ne font aucune hypothèse a priori sur le mode héréditaire de transmission de la maladie. Une des méthodes est également une analyse de liaison qui repose sur le principe du partage d'allèles. Elle tente à montrer que pour des apparentés qui se ressemblent pour un trait (la maladie), la transmission d'un ou des segments chromosomiques ne correspond pas à celle obtenue lors d'une ségrégation aléatoire mendélienne mais qu'au contraire ces apparentés héritent d'un même segment chromosomique parental plus souvent que ne le voudrait le hasard. En d'autres termes, si un marqueur analysé est proche du locus du gène incriminé, les apparentés atteints auront tendance à partager le même segment et donc les mêmes allèles à ce site. Ces apparentés présenteront donc un excès d'allèles du marqueur en commun.
Selon ce principe, la méthode a été appliquée sur les paires de germains atteints de la même maladie (Affected Sibling Pairs, ASP)[Penrose, 1935].
Cette méthode des paires de germains se base sur le fait que s'il existe une liaison, une transmission non aléatoire des allèles parentaux est observée chez les enfants atteints. Dans ce cas, les enfants atteints héritent plus souvent des mêmes allèles du locus considéré que ne le voudrait le hasard. L'allèle commun entre deux germains provenant d'un même allèle parental est dit "identique par descendance" (idendical by descent, IBD) [Campion, 2001,Feingold, 2005]. Cette méthode évalue, pour un marqueur donné, la proportion du nombre d'allèles identiques par descendance au sein de paires de patients. Ainsi, pour un marqueur, les germains peuvent avoir en commun 2, 1 ou 0 allèles IBD hérités de leurs parents. Les germains qui partagent deux allèles IBD (IBD2) ont hérité des deux mêmes allèles de leurs deux parents. S'ils partagent un allèle IBD (IBD1), ils ont hérité du même allèle d'un même parent. Et enfin, ils ne partagent aucun allèle IBD (IBD0) s'ils héritent d'allèles différents. Dans le cas d'une ségrégation mendélienne (en absence de liaison), les germains vont hériter de 2 allèles IBD d'un locus donné dans 25% des cas, d'un allèle IBD dans 50% des cas, et de 0 allèles IBD dans les 25% restants. Ces distributions attendues sont alors comparées aux distributions observées par un simple test de 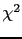 qui devient significatif en cas de liaison (Figure 1.5Différents états IBD possibles pour une paire de germains atteints). Un autre test, plus puissant qui teste spécialement l'augmentation du partage est le 'test moyen' [Blackwelder and Elston, 1985]. Pour tous ces tests, l'augmentation du partage des allèles identiques par descendance chez les paires de germains indique une liaison génétique entre le marqueur et le gène de prédisposition.
qui devient significatif en cas de liaison (Figure 1.5Différents états IBD possibles pour une paire de germains atteints). Un autre test, plus puissant qui teste spécialement l'augmentation du partage est le 'test moyen' [Blackwelder and Elston, 1985]. Pour tous ces tests, l'augmentation du partage des allèles identiques par descendance chez les paires de germains indique une liaison génétique entre le marqueur et le gène de prédisposition.
Ne requérant aucune hypothèse sur le modèle génétique de transmission, cette approche est largement utilisée dans le cas d'études de maladies complexes. Cette approche a permis d'ailleurs de mettre en évidence la liaison du système HLA avec différentes maladies auto-immunes, telles que la sclérose en plaques ou le diabète insulinodépendant (DID) [Demenais et al., 1996]. Même si cette méthode
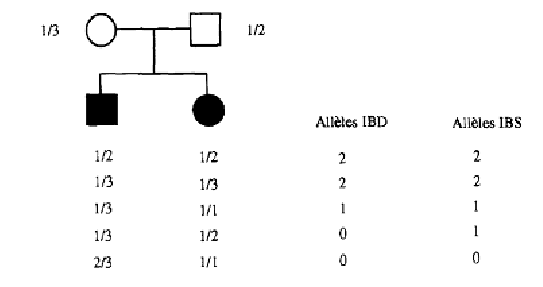
Figure 1.6:
Relation entre allèles IBD et allèles IBS dans un système de 3 allèles
(D'après [Seboun, 1996])
 |
s'affranchit du problème de "pénétrance incomplète" en n'étudiant que des sujets atteints, elle reste une méthode de faible puissance car elle n'étudie qu'un seul type d'apparentement, rendant difficile la séparation entre la concordance des allèles entre germains de la probabilité de ségrégation au hasard des deux loci.
Plusieurs facteurs influencent la puissance d'analyse de cette méthode pour détecter un locus de susceptibilité: l'effet génétique du locus "maladie", la taille de l'échantillon étudié, le taux de recombinaison 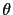 et la détermination de l'état IBD. La baisse de puissance de cette méthode dépend également de l'hétérogénéité génétique de la maladie (présence de plusieurs loci) et de la présence de phénocopies. En ôtant ces derniers, la méthode pour détecter une région d'intérêt résulte de la contribution du locus dans le phénotype et par conséquent du risque relatif familial. Plus la contribution de ce locus sera grande, plus cette méthode pourra le détecter. Ce facteur intervient aussi dans la taille de l'échantillon à tester. Plus la contribution sera faible, plus la taille de l'échantillon à tester sera importante. Par exemple, en utilisant des marqueurs complètement informatifs et en supposant l'absence de recombinaison (conditions idéales), au moins 200 paires de germains sont nécessaires pour détecter une liaison avec une puissance de 80% pour une valeur de P de 0.05 si
et la détermination de l'état IBD. La baisse de puissance de cette méthode dépend également de l'hétérogénéité génétique de la maladie (présence de plusieurs loci) et de la présence de phénocopies. En ôtant ces derniers, la méthode pour détecter une région d'intérêt résulte de la contribution du locus dans le phénotype et par conséquent du risque relatif familial. Plus la contribution de ce locus sera grande, plus cette méthode pourra le détecter. Ce facteur intervient aussi dans la taille de l'échantillon à tester. Plus la contribution sera faible, plus la taille de l'échantillon à tester sera importante. Par exemple, en utilisant des marqueurs complètement informatifs et en supposant l'absence de recombinaison (conditions idéales), au moins 200 paires de germains sont nécessaires pour détecter une liaison avec une puissance de 80% pour une valeur de P de 0.05 si 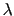 s=2 (ce qui correspond déjà à une valeur élevée pour des facteurs de risque pour des maladies complexes), alors que 60 paires de germains suffisent si
s=2 (ce qui correspond déjà à une valeur élevée pour des facteurs de risque pour des maladies complexes), alors que 60 paires de germains suffisent si 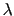 s=5 [Risch, 1990].
s=5 [Risch, 1990].
Elle dépend aussi du taux de recombinaison entre les deux loci marqueur-maladie. Par exemple, sur un échantillon de 300 paires de germains, la puissance de détection d'une liaison statistique diminue de moitié lorsque le taux de recombinaison 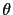 est supposé être de 0.10 [Risch, 1990].
est supposé être de 0.10 [Risch, 1990].
La puissance de cette approche dépend aussi de la détermination sans ambigüité de la provenance parentale de chaque allèle, c'est-à-dire, de l'état IBD des allèles du marqueur. Cette détermination correcte des allèles transmis des parents n'est possible qu'avec l'étude de marqueurs hautement polymorphes et celle du génotype des parents. Si ce dernier n'est pas réalisable, l'étude du génotype des individus supplémentaires de la fratrie est utile pour pouvoir "évaluer" les génotypes parentaux manquants. Cependant, dans la plupart des cas, les données de génotype aux locus "marqueurs" sont souvent ambiguës, ne permettant pas de connaître la provenance parentale exacte de chaque allèle. C'est le cas avec des parents homozygotes : les deux germains ont-il reçu le même allèle ou différentes copies de l'allèle? Il est seulement possible de déterminer si deux germains ont les mêmes allèles du marqueur identique par état (identical by state, IBS). Deux allèles sont définis comme étant identique par état lorsqu'ils sont les mêmes, indépendamment de leur origine ancestrale (Figure 1.6Relation entre allèles IBD et allèles IBS dans un système de 3 allèles).
Pour cette raison, plusieurs tests basés sur le partage IBS ont été proposés, consistant à compter les allèles concordants entre germains atteints. Une des méthodes fondées sur le statut IBS est la méthode APM (affected pedigree member method) [Weeks and Lange, 1988]. Cette méthode permet d'étudier le statut IBS sur tous les sujets atteints appartenant à des généalogies, y compris de parents éloignés. Même si pour un marqueur très polymorphe, le statut IBS est similaire au statut IBD, ces méthodes sont moins robustes dans la majorité des cas car elles dépendent de la fréquence allélique du marqueur. En effet, pour calculer les fréquences attendues du partage IBS sous l'hypothèse nulle (en l'absence de liaison), il est nécessaire d'estimer les fréquences alléliques dans la population, paramètres souvent difficiles à établir avec précision. Une erreur sur ces fréquences peut conduire à la détection fausse d'une liaison. Récemment, d'autres méthodes plus flexibles, certaines basées sur le maximum de vraisemblance (MLS, Maximum Likelihood Score), permettent d'estimer le partage IBD et de prendre en compte les situations plus complexes telles que la présence de marqueurs "ambigus", l'étude de différents types de parentés atteints, l'absence de génotypes d'un parent. Dans ces méthodes, les proportions du partage IBD sont calculées en considérant tous les génotypes possibles pour les parents qui seraient en accord avec les données. L'ensemble de ces nouvelles méthodes permettent aussi de traiter les familles dans lesquelles il y a soit de multiples germains (comme la méthode MLB, Maximum Likelihood Binomial method) soit plusieurs membres (la généralisation du test moyen, la méthode NPL, Non Parametric Linkage), atteints et pas nécessairement indépendants [Abel and Muller-Myhsok, 1998].
Selon la méthode utilisée, le moyen de corriger cette non-indépendance parmi les germains est différent. Certains analyseront seulement une paire ou des paires indépendantes et, d'autres utiliseront toutes les paires possibles, mais en pondérant leurs contributions au test selon le nombre d'individus atteints dans les germains. L'effet de la non indépendance sur le test de liaison varie selon la méthode utilisée mais par exemple, dans le cas de la méthode MLB, l'erreur de type I (erreur de rejeter l'hypothèse nulle alors qu'elle est vraie, c'est-à-dire affirmer une liaison alors qu'il n'y en a pas) peut être augmentée [Abel and Muller-Myhsok, 1998]. De plus, certaines méthodes utilisent simultanément l'information de tous les marqueurs sur le chromosome. Cette analyse "multipoint" permet, comme pour une analyse paramétrique, d'augmenter la puissance dans les meilleures conditions mais également d'améliorer l'estimation du partage IBD. Cette analyse reste néanmoins limité aux algorithmes utilisés qui peuvent être sensibles à la quantité de marqueurs et à la complexité des familles étudiées.
Les méthodes non paramétriques ont également été utilisées pour des analyses de liaison à un trait quantitatif (QTL, Quantitative Trait Loci). Proposée par Haseman et Elston (1972), cette approche est basée sur la corrélation entre le statut IBD des germains à un marqueur et leur ressemblance phénotypique (trait clinique ou biologique), mesurée par la différence au carré entre les valeurs quantitatives du trait [JK. and RC., 1972]. Plusieurs variantes de cette méthode existent dont une fondée sur la décomposition de la variance.
Les analyses de liaison non paramétrées sont réalisées entre autres avec différents programmes tels que GeneHunter [Kruglyak et al., 1996], Merlin [Abecasis et al., 2002] ou SIMWALK2 [Sobel and Lange, 1996].
Enfin, la méthode générale des paires de germains n'est généralement pas capable de localiser un gène avec précision. En effet, le manque de puissance de cette méthode pour la détection de gènes ayant un effet mineur entraîne souvent la détection de fausses régions de prédisposition (faux-positifs), pouvant expliquer le peu de réplication des loci initialement suggérés. Et même si ces méthodes non paramétriques ont permis d'identifier surtout des régions d'intérêt contenant des gènes à effet fort, les régions identifiées ne sont souvent pas suffisamment petites (10 à 30 cM) pour permettre le clonage positionnel facile du gène causal, quelles que soient les approches utilisées (criblage systématique du génome ou cartographie fine) [Risch and Merikangas, 1996]. L'approche suivante sera alors la recherche d'association allélique (ou d'un ensemble d'allèles ("association haplotypique")), dans la population générale, entre la maladie et les allèles de marqueurs bi-alléliques présents soit dans les régions de prédisposition pour une cartographie fine, ou soit dans les gènes candidats pour une stratégie gène-candidat. Elle peut également être utilisée comme alternative des analyses de liaison lors d'un criblage du génome, avec des SNPs répartis sur le génome entier.



Next: Analyses d'association
Up: Méthodes utilisées
Previous: Méthodes utilisées
Contents
anouar
2009-08-22

