Principe des études d'association

Comme précédemment décrit dans le chapitre Introduction, les études d'association sont fondées sur le principe d'un déséquilibre de liaison (DL). Le déséquilibre de liaison décrit une non-indépendance de deux allèles situés à des loci différents du génome dans la population. Il est affecté par la recombinaison méiotique et diminue proportionnellement à la distance séparant les loci.
La force du déséquilibre de liaison entre deux locus est mesurée à l'aide du coefficient de déséquilibre de liaison, D. Considérons le cas de deux marqueurs bialléliques, avec les allèles A, a et B, b de fréquence $p_{A}, q_{A}, p_{B}$ et $q_{B}$. Ce coefficient D correspond à la différence entre la proportion observée d'un haplotype et celle attendue sous l'hypothèse d'indépendance.
Dans le cas de l'haplotype $AB$ : $D= P(AB)_{\text{observé}}-P(AB)_{\text{attendu}}$ , si les deux locus sont indépendants, on s'attend à ce que la proportion d'haplotypes AB soit égale au produit des fréquences d'allèles $A$ et $B$, c'est-à-dire :

$D= P(AB)_{\text{observé}}-P(AB)_{\text{attendu}} = P(AB)_{\text{observé}} -p_{A}p_{B}$

Mais D est également estimé par:
$D= P(Ab)_{\text{observé}} -P(Ab)_{\text{attendu}} = P(Ab)_{\text{observé}} - p_{A}q_{B}$
$D= P(aB)_{\text{observé}} -P(aB)_{\text{attendu}} = P(aB)_{\text{observé}} - q_{A}p_{B}$
$D= P(ab)_{\text{observé}} -P(ab)_{\text{attendu}} = P(ab)_{\text{observé}} - q_{A}q_{B}$
$D= P(AB)P(ab) - P(Ab)P(aB)$

Ainsi, plus $D$ est élevé, plus les locus sont en déséquilibre de liaison.
Afin d'avoir des mesures comprises entre $0$ et $1$, des standardisations de $D$ ont été proposées, dont deux sont les plus utilisées: le coefficient $D'$ et le coefficient de corrélation $r^{2}$. Ils sont calculés ainsi:

$\vert D'\vert=\vert D\vert/D_{max}$
où $D_{max} = \min(p_{A}q_{B}, q_{A}p_{B})$ si $D>0$
$D_{max} =min(p_{A}p_{B}, q_{A}q_{B})$ si $D<0$
et $r^{2} = D^{2} / (p_{A}q_{A}p_{B}q_{B})$

Lorsque $D'=1$, il y a déséquilibre complet et lorsque $r^{2}=1$, il y a déséquilibre parfait.
La mesure $r^{2}$ varie, comme D', avec la recombinaison mais aussi avec la fréquence allélique des marqueurs, qui est un reflet de leur ancienneté dans l'histoire d'une

Figure 2.3: Approche "TagSNPs" se fait en trois étapes
(a) Les polymorphismes nucléotidiques simples (SNP) sont identifiés dans les échantillons d'ADN provenant de nombreux individus. (b) Les SNPs adjacents qui sont hérités simultanément sont regroupés en "haplotypes" dont la fréquence dans la population excède un pour cent. (c) Des SNPs marqueurs, au sein d'un haplotype, sont choisis pour constituer un identificateur unique de cet haplotype. En génotypant les trois SNPs marqueurs illustrés dans cette figure, on peut déterminer lequel des quatre haplotypes illustrés est porté par chaque individu. (D'apprès le site: http://www.hapmap.org/whatishapmap.html.fr)

population. Ainsi, contrairement au cas où $D'=1$, deux SNPs ayant un $r^{2}$ de 1 sont totalement équivalents et l'un peut être utilisé comme substitut de l'autre (l'information contenue est équivalente). Ceci est dû à la présence de seulement deux des génotypes possibles. En pratique, un $r^{2}$ de 0,8 est habituellement choisi dans les études d'association pour décrire deux SNPs équivalents.
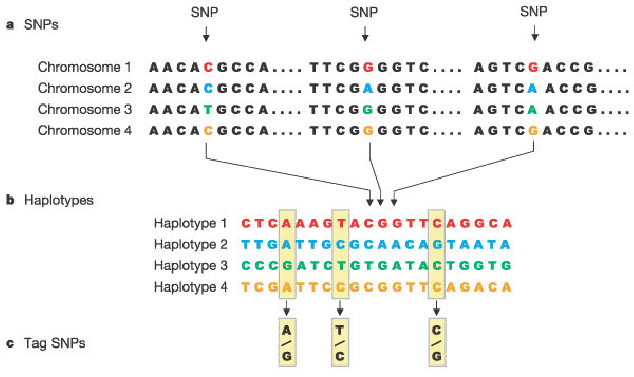
L'étude du DL au sein du génome montre que le DL peut parfois s'étendre sur plusieurs centaines de kilobases. Le génome est d'ailleurs structuré en fonction du DL, résultant d'une différence du taux de recombinaison le long du génome. Cette structuration en blocs de DL peut aussi résulter de phénomènes dépendants de la population étudiée tels que la dérive génétique (fixation d'un allèle de manière aléatoire au sein de la population), la croissance et la stratification de la population, la sélection naturelle et l'apparition de mutations. Le génome est donc organisé en blocs de régions transmises de manière intacte au cours des générations. Ces blocs dans lesquels il existe un fort DL et par conséquent, une faible diversité haplotypique (soit les différentes combinaisons possibles des allèles de chaque SNP) sont appelés des blocs de DL (ou blocs haplotypiques). Ainsi, par l'existence de ce fort DL, de nombreux polymorphismes donnent la même information sur la variation génétique au sein du bloc car ils sont souvent hérités ensemble. Par conséquent, seulement quelques polymorphismes seront nécessaires à étudier car ils seront représentatifs de l'ensemble des haplotypes existants dans la population, c'est-à-dire de l'ensemble de la variabilité génétique du bloc. Ils sont nommés "TagSNPs" (Figure 2.3Approche "TagSNPs" se fait en trois étapes).
La caractérisation des SNPs, en particulier des TagSNPs, a été l'objectif de différents projets d'analyse du génome dont HapMap (http://www.hapmap.org/) afin de faciliter les études d'association [Consortium, 2003]. Ce projet international a permis de cataloguer les variations génétiques (nature, position et fréquence selon les populations) les plus fréquentes chez l'Humain, en analysant l'ADN de 4 populations d'origine africaine, asiatique (japonaise et chinoise) et européenne [Consortium, 2003]. Cette connaissance permet l'identification de la plupart des haplotypes communs à la population mondiale, variables en fréquence selon les populations. Ainsi, l'étude des blocs DL en fonction des populations permet de caractériser les identificateurs uniques d'un haplotype, les TagSNPs, spécifique d'une population [Consortium, 2005]. Cela est très utile pour des études d'association systématiques.