


Next: ANALYSE D'ASSOCIATION
Up: Méthodes des analyses de
Previous: Analyse paramétrique
Contents
En plus des analyses paramétriques, différentes analyses non paramétriques multipoints ont été réalisées car ce type d'analyse ne nécessite pas de connaître les paramètres déjà décrits précédemment. Une analyse multipoint est plus robuste qu'une analyse bi-point car elle prend en compte les informations obtenues par tous les marqueurs, même ceux qui sont peu informatifs en se basant sur les marqueurs voisins.
Différents programmes permettent de faire ce type d'analyse tels que GENEHUNTER [Kruglyak et al., 1996], Allegro [Gudbjartsson et al., 2000], ou MERLIN [Abecasis et al., 2002]. Cependant, dans le cas de l'étude sur des grandes familles, peu de programmes peuvent les analyser à moins d'avoir un nombre limité de marqueurs tels que LINKAGE [Lathrop et al., 1984] et SIMWALK [Sobel and Lange, 1996]. Pour le premier criblage, deux méthodes non paramétriques multipoints ont été utilisées : la méthode MLB (Maximum Likelihood Binomial method) [Abel and Muller-Myhsok, 1998] et la méthode NPL (Non Parametric Linkage). Ces deux méthodes sont des extensions de la méthode des paires de germains atteints, décrite dans le chapitre Introduction et consistent à déterminer l'IBD entre tous les germains atteints (dans le cas du MLB) ou entre toutes les paires de germains atteints (dans le cas du NPL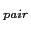 ) ou encore entre tous les malades d'une famille (dans le cas du NPL
) ou encore entre tous les malades d'une famille (dans le cas du NPL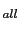 ) . Cette approche permet d'accorder plus d'importance à une transmission d'un même allèle à plusieurs apparentés atteints qu'à la transmission d'un certain allèle à une paire de germains atteints.
) . Cette approche permet d'accorder plus d'importance à une transmission d'un même allèle à plusieurs apparentés atteints qu'à la transmission d'un certain allèle à une paire de germains atteints.
Contrairement au NPL qui est basé sur le nombre d'allèles partagés IBD par tous les membres atteints d'une famille, la méthode MLB est basée sur la distribution binomiale des allèles parentaux parmi les descendants atteints, considérant ainsi tous les germains pris comme un entier.
La probabilité 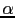 pour un germain atteint de recevoir d'un parent l'allèle "marqueur" transmis avec l'allèle "maladie" est égale à 0.5 sous l'hypothèse nulle de non liaison et est supérieure à 0.5 sous l'hypothèse de liaison. Le test de liaison est réalisé à partir d'un test de rapport de vraisemblance
pour un germain atteint de recevoir d'un parent l'allèle "marqueur" transmis avec l'allèle "maladie" est égale à 0.5 sous l'hypothèse nulle de non liaison et est supérieure à 0.5 sous l'hypothèse de liaison. Le test de liaison est réalisé à partir d'un test de rapport de vraisemblance
![$\lambda = 2Ln[L(\alpha)/L(\alpha = 0.5)]$](img73.png) avec une statistique distribuée asymptotiquement comme une distribution mixte de
avec une statistique distribuée asymptotiquement comme une distribution mixte de
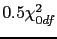 et
et
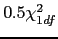 . Le test peut également être exprimé comme Z
. Le test peut également être exprimé comme Z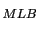 =
=
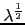 ou LOD MLB =
ou LOD MLB =
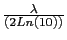 .
.
Ces analyses sont réalisables grâce aux programmes MLBGH, une extension du programme GENEHUNTER, et MERLIN. Un des inconvénients de ces programmes est la limite du nombre maximal d'individus pouvant être analysés. Ainsi, pour permettre l'analyse, les structures familiales ont été modifiées en les clivant en familles nucléaires avec le program Mega 2 [Mukhopadhyay et al., 2005]. Les 45 familles ont été divisées en 77 familles nucléaires, chacune avec au moins deux germains atteints.
Après l'étude de ce premier criblage, un tour du génome a été effectué, non plus sur les 14 premières familles du Lot I mais sur la totalité des 45 familles du Lot I. Afin de pouvoir comparer avec le premier criblage, nous avons étudié ce deuxième tour de génome seul (Criblage 2) ou en ajoutant les marqueurs du premier criblage (Criblage 1+2) en utilisant la méthode MLB.
Pour l'analyse du deuxième criblage avec ou sans les marqueurs du premier criblage, d'autres méthodes non paramétriques multipoints (en particulier en calculant les statistiques NPL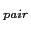 et NPL
et NPL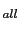 ) ont été appliquées pour l'analyse des familles non fragmentées grâce au programme SIMWALK2 [Sobel and Lange, 1996]. Contrairement au programme MERLIN, SIMWALK2 utilise une approche MCMC (Markov Chain Monte Carlo) pour estimer les allèles IBD entre individus atteints selon leur vraisemblance.
) ont été appliquées pour l'analyse des familles non fragmentées grâce au programme SIMWALK2 [Sobel and Lange, 1996]. Contrairement au programme MERLIN, SIMWALK2 utilise une approche MCMC (Markov Chain Monte Carlo) pour estimer les allèles IBD entre individus atteints selon leur vraisemblance.
La difficulté de ces analyses reste l'estimation du statut IBD des individus. Contrairement aux analyses de paires de germains, l'utilisation de nombreux individus atteints dans l'analyse, permet une meilleure estimation de ce statut, ainsi que l'utilisation simultanée de l'information de tous les marqueurs sur le chromosome. Néanmoins, selon la méthode utilisée, le moyen de corriger l'effet de la non-indépendance parmi les germains dans l'analyse est différent. Dans tous les cas, une mauvaise estimation du statut IBD peut diminuer la puissance d'analyse et amener à des faux-positifs. Le seuil de la valeur de P doit être au moins égale à 7.4 x 10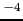 (correspondant à un lod score=2.2) pour indiquer une preuve suggestive d'une liaison, à 2.2 x 10
(correspondant à un lod score=2.2) pour indiquer une preuve suggestive d'une liaison, à 2.2 x 10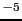 (lod score=3.6) pour une preuve significative et à 3 x 10
(lod score=3.6) pour une preuve significative et à 3 x 10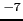 (lod score=5.4) pour une preuve hautement significative [Lander and Kruglyak, 1995]. Cependant, à l'exception de l'étude du premier criblage sur 14 familles où la valeur de P est de 1%, la valeur de P seuil dans l'ensemble des études de liaison, est de 5% (Z
(lod score=5.4) pour une preuve hautement significative [Lander and Kruglyak, 1995]. Cependant, à l'exception de l'étude du premier criblage sur 14 familles où la valeur de P est de 1%, la valeur de P seuil dans l'ensemble des études de liaison, est de 5% (Z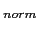 =1.6 pour la méthode MLB). Conscients des erreurs possibles, nos résultats n'ont pas été corrigés en fonction du nombre de tests effectués (Correction de Bonferonni).
=1.6 pour la méthode MLB). Conscients des erreurs possibles, nos résultats n'ont pas été corrigés en fonction du nombre de tests effectués (Correction de Bonferonni).



Next: ANALYSE D'ASSOCIATION
Up: Méthodes des analyses de
Previous: Analyse paramétrique
Contents
anouar
2009-08-22